Ridiculous strawberry picking

Please use a newer browser to see the simulation.

0

T:

My wonder button is being pushed all the time.

Try again Continue

Sun's mass: 1.00

Carl’s experiment

Thursday noon of 23 October 1997. Doctor Carl Cox smashes a ripe strawberry lying on his laboratory desk with his forehead and shouts “It is wonderful!”

What just happened today to Carl — and, consequently, to everything else in the vicinity of the 100,000 galaxies within the Laniakea Supercluster — is quite remarkable and is worth explaining. Doctor Carl has just discovered a way of increasing the mass of the Sun by feeding it the dark energy from the area in space stretching billions and billions of light years. This trick, bizarrely, involves berries from the local grocery shop and works both ways: the Sun’s mass can also be reduced by pumping it back into the surrounding area of the Universe.

Carl approaches a big shiny metallic box with blinking buttons and pushes several of them. A warning message box “Are you sure you want to execute the big_sun script?” appears on the screen of the apparatus. Without hesitation Carl presses the “Enter” button and returns to his desk with a satisfied grin. He wipes off berry juice from his forehead with a manuscript of a finished paper titled “Cross pollination of honeysuckles in zero gravity by Australian longhorn beetles” that was planned to be submitted to the Astrobotanical Review journal. This paper is not important anymore. Nothing really is.

Orbital distance and Newton’s Law of Universal Gravitation

The short-term implications of this experiment are obvious to any student who attended an introductory astronomy class. What happens to the Earth if the mass of the Sun increases? One of the most fundamental laws, Newton’s Law of Universal Gravitation, tells us that the force of attraction between two bodies is proportional to the product of their masses and inversely proportional to the square of the distance between them [1, p. 131]. This law implies, that if Carl increases the mass of the Sun, it will exert stronger gravitational force on the Earth. As a result, the Earth moves closer to the Sun (see Figure 1).

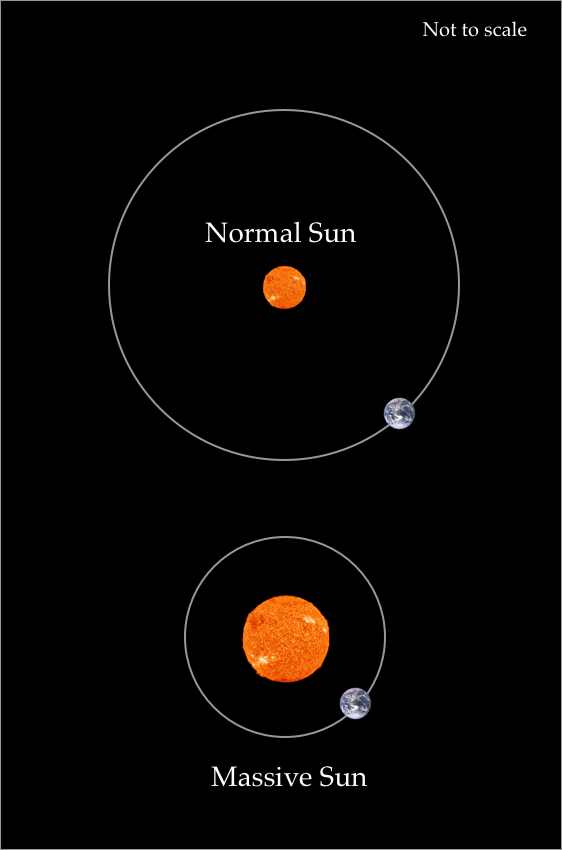
Figure 1: The Earth is closer to the more massive Sun.

Orbital period and Kepler’s third law

Everybody knows that it takes about 365 days for the Earth to complete one full circle around the Sun. We call this time ‘a year’ and astronomers call it the Earth’s orbital period. But what happens to Earth’s orbital period as the planet moves closer to the Sun? This question can be answered by using Kepler’s third law [2, p. 27] that states — closer planets have smaller orbital periods. Therefore, the increase in Sun’s mass will result in shorter year on the Earth.

The Sun’s luminosity

The increase in Sun’s mass also affects its brightness, which is also called ‘luminosity’. This happens because larger mass creates bigger gravitational pressure in its core, which increases the rate of fusion reactions and creates more light. How much brighter the Sun becomes if Carl doubles its mass? Figure 2 demonstrates that the Sun will be about eight times brighter, because the luminosity of a star similar to the Sun is roughly proportional to the cube of its mass [3].

Figure 2: The bigger Sun is much brighter.

Habitable zone

As we’ve shown, the planets receive more sunlight as the Sun’s mass increases. As a result, if the Earth’s distance to the Sun does not change, its average global temperature will increase. If it gets too hot, Earth’s oceans will start to boil and that will probably be the death sentence to all animal life on the surface of our planet. In astronomy, the range of distances from a star at which liquid water can exist on the surface of a planet is called the star’s habitable zone. As Doctor Carl increases the mass of the Sun, its habitable zone moves farther away.

We can see from Figure 3 that massive Sun would have more distant habitable zone. In this case, the Earth would be too close to the Sun, and the water would boil and evaporate. Therefore, Carl Cox needs to be very careful and try not to keep Sun’s mass high for too long.

Figure 3: The habitable zone of the bigger Sun is farther away.

The dark energy and the expansion of the Universe

The dark energy is a term astronomers use to explain the observed expansion of the Universe [2, p. 726]. At this point astrophysicists do not have a clue what this dark energy actually is, nor they were able to detect it. The idea is that there is a mysterious uniform substance that fills all of space in the Universe and pushes the Universe apart. As a result, the galaxies which are not close enough to have strong gravitational attraction are moving away from each other.

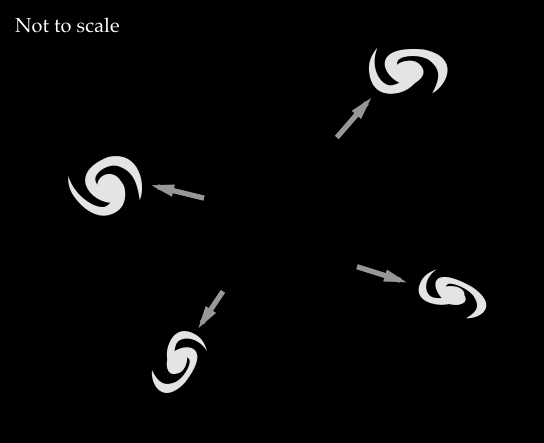
Figure 4: Dark energy makes space bigger.

What would happen if Carl Cox took some of this dark energy and converted it into Sun’s mass? If such a trick was possible, the space would stop inflating and start collapsing. This would, consequently, make the space smaller with time making the galaxies approach each other with increasing speeds. Would it be a good thing? Possibly, but if there is a space real estate market — the contraction will make the available space smaller and drive the prices up. And that can make some alien real estate buyers very, very unhappy.

Credits

1. Editor in chief: Emily Saaen.

2. “The Blue Marble” image: NASA/Apollo 17 crew; taken by either Harrison Schmitt or Ron Evans, source, source.

3. “The Sun photographed at 304 angstroms” image: NASA/SDO (AIA), source, source.

References

• [1]. J. Bennet, M. Donahue, N. Schneider , and M. Voit, Cosmic perspective. United Kingdom: Pearson Education Limited, 2014.

• [2]. J. Bennett, G. Shostak, Life in the Universe, 4th ed. San Francisco, CA: Pearson, 2016.

• [3]. “Mass-luminosity relationship”. Hyperphysics.

• [4]. The complete source code of the game.

• [5]. Programming a simulation of the Earth orbiting the Sun.